天一大联考2024-2025学年高中毕业班阶段性测试(一)数学试卷答案,我们目前收集并整理关于天一大联考2024-2025学年高中毕业班阶段性测试(一)数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

天一大联考2024-2025学年高中毕业班阶段性测试(一)数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

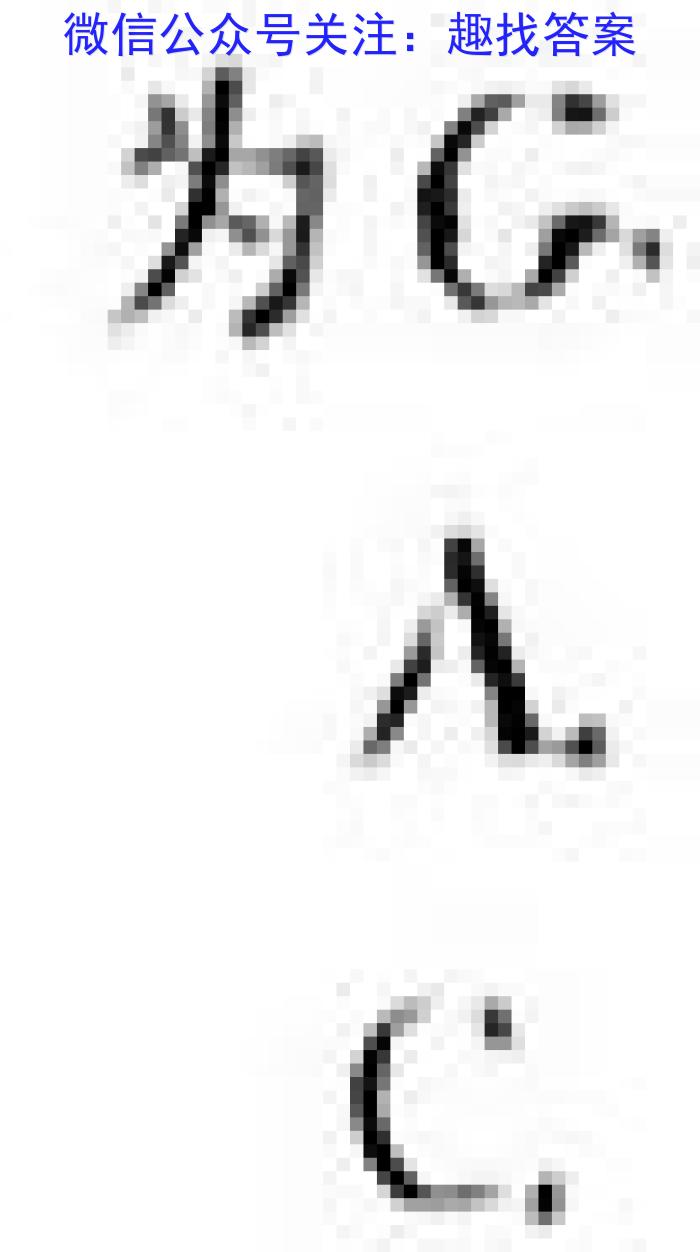
9.2023年2月10日,远在火星执行全球遥感科学探测任务的“天问一号”火星环绕器(以下简称环绕器),已经在火星“上岗"满两年,作为一位功能强大的“太空多面手”,环绕在“天向一号”火星探测任务中,分饰了飞行器、通信器和探测器三大角色、创下多项图内外首次记录。若已知环绕器绕火星做匀速圆周运动的轨逐半径为、周期为T.火星的半径为R.引力常量为G.A.C.C.

分析由题意可得f（x）在（-∞，0]递增，由奇函数的性质可得，f（x）在R上递增，原不等式即为f（m•3^x）＜-f（3^x-9^x-2）=f（9^x-3^x+2），即有m•3^x＜9^x-3^x+2，令t=3^x（t＞0），转化为t的不等式，运用参数分离和基本不等式可得最小值，进而得到m的范围．

解答解：对一切x∈（-∞，0]恒满足f′（x）≥0，
即有f（x）在（-∞，0]递增，
由奇函数的性质可得，f（x）在R上递增，
f（m•3^x）+f（3^x-9^x-2）＜0，即为
f（m•3^x）＜-f（3^x-9^x-2）=f（9^x-3^x+2），
即有m•3^x＜9^x-3^x+2，
令t=3^x（t＞0），即有mt＜t²-t+2，
则m＜t+$\frac{2}{t}$-1的最小值，由t+$\frac{2}{t}$-1≥2$\sqrt{2}$-1．
当且仅当t=$\sqrt{2}$时，取得最小值．
则m＜2$\sqrt{2}$-1．即m的取值范围是（-∞，2$\sqrt{2}$-1）．

点评本题考查奇函数的定义和性质，考查不等式恒成立问题的解法，注意运用参数分离和基本不等式求最值，属于中档题．