2024年高考真题(天津卷)数学试卷答案,我们目前收集并整理关于2024年高考真题(天津卷)数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

2024年高考真题(天津卷)数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

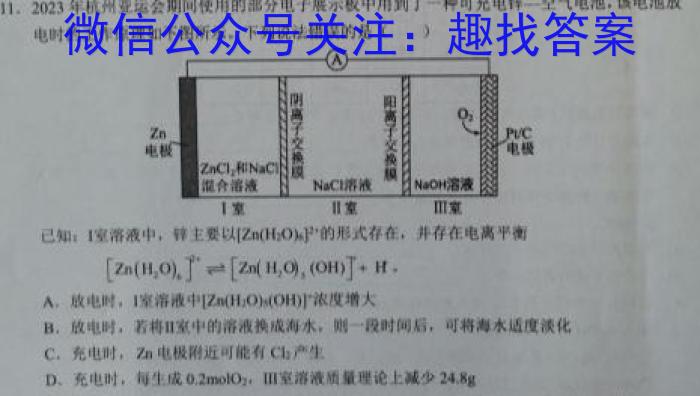
11.2023年杭州亚运会期间使用的部分电子展示板中用到了一种可充电锌一空气电池,该电池放电时的工作原理如下图所示,下列说法错误的是()已知:I室溶液中,锌主要以[Zn(H2O)6]^2+*的形式存在,并存在电离平衡[Zn(H2O)4]Zn(H2O),(OH)]+H.A.放电时,I室溶液中[Zn(H2O)5(OH)]浓度增大B.放电时,若将I室中的溶液换成海水,则一段时间后,可将海水适度淡化C.充电时,电极附近可能有Cl2产生D.充电时,每生成0.2molO2,Ⅲ室溶液质量理论上减少24.8g

分析（1）由f（x）=0进行求解即可；
（2）根据函数奇偶性的定义进行判断即可判断函数f（x）的奇偶性；
（3）根据函数单调性的定义结合指数函数单调性的性质即可得到结论．

解答解：（1）由f（x）=${a}^{x}-\frac{1}{{a}^{x}}$=0得a^x=$\frac{1}{{a}^{x}}$，即（a^x）²=1，则a^x=1，解得x=0，
即函数f（x）有零点，其中零点为0；
（2）函数的定义域为（-∞，+∞），
则f（x）=a^x-$\frac{1}{{a}^{x}}$=a^x-a^-x，
则f（-x）=a^-x-a^x=-（a^x-a^-x）=-f（x），
则函数f（x）为奇函数；
（3）a＞1时，函数f（x）为增函数，当0＜a＜1时，函数f（x）为减函数．
证明：设x₁＜x₂，
f（x₁）-f（x₂）=${a}^{{x}_{1}}$-$\frac{1}{{a}^{{x}_{1}}}$+-${a}^{{x}_{2}}$+$\frac{1}{{a}^{{x}_{2}}}$=（${a}^{{x}_{1}}$-${a}^{{x}_{2}}$）+$\frac{1}{{a}^{{x}_{2}}}$-$\frac{1}{{a}^{{x}_{1}}}$=（${a}^{{x}_{1}}$-${a}^{{x}_{2}}$）+$\frac{{a}^{{x}_{1}}-{a}^{{x}_{2}}}{{a}^{{x}_{1}}•{a}^{{x}_{2}}}$
=（${a}^{{x}_{1}}$-${a}^{{x}_{2}}$）（1+$\frac{1}{{a}^{{x}_{1}}•{a}^{{x}_{2}}}$），
若a＞1，∵x₁＜x₂，
∴${a}^{{x}_{1}}$＜${a}^{{x}_{2}}$，即${a}^{{x}_{1}}$-${a}^{{x}_{2}}$＜0，1+$\frac{1}{{a}^{{x}_{1}}•{a}^{{x}_{2}}}$＞0，
∴f（x₁）-f（x₂）＜0，
即f（x₁）＜f（x₂），
故f（x）在（-∞，+∞）上单调递增；
若0＜a＜1，∵x₁＜x₂，
∴${a}^{{x}_{1}}$＞${a}^{{x}_{2}}$，即${a}^{{x}_{1}}$-${a}^{{x}_{2}}$＞0，1+$\frac{1}{{a}^{{x}_{1}}•{a}^{{x}_{2}}}$＞0，
∴f（x₁）-f（x₂）＞0，
即f（x₁）＞f（x₂），
故f（x）在（-∞，+∞）上单调递减．
即a＞1时，函数f（x）为增函数，当0＜a＜1时，函数f（x）为减函数．

点评本题主要考查函数零点的求解，函数奇偶性和单调性的判断和证明，利用函数奇偶性和单调性的定义是解决本题的关键．