2024届国考1号15第15套高考适应性考试(五)数学试卷答案,我们目前收集并整理关于2024届国考1号15第15套高考适应性考试(五)数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

2024届国考1号15第15套高考适应性考试(五)数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

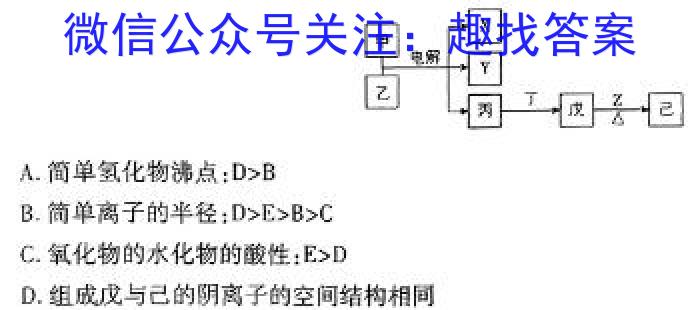
5.短周期主族元素A、B、C、D、E原子序数依次增大,甲、乙、丙、丁、戊、己是由这些元素组成的化合物,X、Y、Z是由这些元素组成的单质。A与C、B与D同主族。甲与丙由10电子微粒构成,己常用作脱氯剂,其溶液在酸性环境下会生成淡黄色浑浊,戊、已两物质化学元素组成相同。上述物质的转化关系如图所示。下列说法正确的是A.简单氢化物沸点:D>BB.简单离子的半径:D>E>B>CC.氧化物的水化物的酸性:E>DD.组成戊与己的阴离子的空间结构相同

分析画出图形，结合图形，得出△VAB是边长为$\sqrt{2}$的等边三角形，利用体积相等求出点C到平面AVB的距离．

解答解：如图所示，
三棱锥V-ABC中，VC⊥平面ACB，∠ACB=90°，VC=AC=BC=1，
∴△VAB是边长为$\sqrt{{1}^{2}{+1}^{2}}$=$\sqrt{2}$的等边三角形，
它的面积为$\frac{1}{2}$×${（\sqrt{2}）}^{2}$×sin60°=$\frac{\sqrt{3}}{2}$；
设点C到平面AVB的距离是h，
则三棱锥的体积是$\frac{1}{3}$•h•S_△VAB=$\frac{1}{3}$•VC•S_△ABC，
解得h=$\frac{1×\frac{1}{2}×1×1}{\frac{\sqrt{3}}{2}}$=$\frac{\sqrt{3}}{3}$，
即C到平面AVB的距离是$\frac{\sqrt{3}}{3}$．
故答案为：$\frac{\sqrt{3}}{3}$．

点评本题考查了空间中距离关系的应用问题，也考查了等积法的应用问题，是基础题目．