安师联盟 安徽省2024年中考仿真极品试卷(二)2数学试卷答案,我们目前收集并整理关于安师联盟 安徽省2024年中考仿真极品试卷(二)2数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

安师联盟 安徽省2024年中考仿真极品试卷(二)2数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

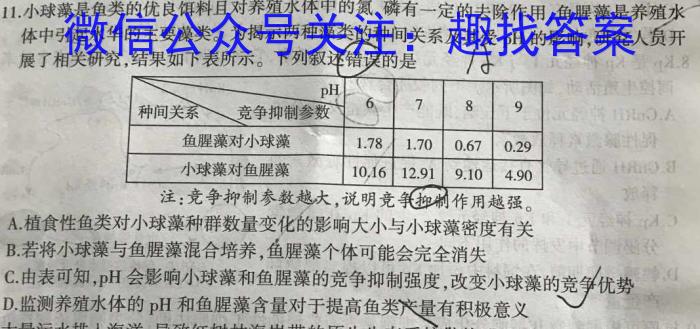
11.小球藻是鱼类的优良饵料且对养殖水体中的氮、磷有一定的去除作用,鱼腥藻是养殖水引起水华的主要藻类。为揭示两种藻类的种间关系及其受pH的影响,研究人员开展了相关研究,结果如下表所示。下列叙述错误的是1小注:竞争抑制参数越大,说明竞争抑制作用越强。A.植食性鱼类对小球藻种群数量变化的影响大小与小球藻密度有关B.若将小球藻与鱼腥藻混合培养,鱼腥藻个体可能会完全消失C.由表可知,pH会影响小球藻和鱼腥藻的竞争抑制强度,改变小球藻的竞争优势D.监测养殖水体的pH和鱼腥藻含量对于提高鱼类产量有积极意义

分析（1）化简得f（x）=2sin（2ωx-$\frac{π}{3}$）+1．由周期=π得ω=1，令-$\frac{π}{2}$+2kπ≤22x-$\frac{π}{3}$≤$\frac{π}{2}$+2kπ，可解出单调递增区间；
（2）由f （A）=$\sqrt{3}$+1解出A，代入余弦定理得出bc的值，代入面积公式S_△ABC=$\frac{1}{2}$bcsinA．

解答解：（1）f（x）=（sinωx+cosωx）²+$\sqrt{3}$（sin²ωx-cos²ωx）
=1+2sinωxcosωx-$\sqrt{3}$（cos²ωx-sin²ωx）
=sin2ωx-$\sqrt{3}$cos2ωx+1=2sin（2ωx-$\frac{π}{3}$）+1．
∴T=$\frac{2π}{2ω}$=π，∴ω=1，
∴f（x）=2sin（2x-$\frac{π}{3}$）+1．
令-$\frac{π}{2}$+2kπ≤22x-$\frac{π}{3}$≤$\frac{π}{2}$+2kπ，解得kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$，
故函数f（x）的单调递增区间为[kπ-$\frac{π}{12}$，kπ+$\frac{5π}{12}$]，k∈Z．
（2）∵f（A）=2sin（2A-$\frac{π}{3}$）+1=$\sqrt{3}$+1，∴sin（2A-$\frac{π}{3}$）=$\frac{\sqrt{3}}{2}$，
∴2A-$\frac{π}{3}$=$\frac{π}{3}$或2A-$\frac{π}{3}$=$\frac{2π}{3}$，
∴A=$\frac{π}{3}$或A=$\frac{π}{2}$（舍）．
∵cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$，
∴$\frac{1}{2}$=$\frac{16-2bc-4}{2bc}$，∴bc=4，
∴S_△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}$×4×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$．

点评本题考查了三角函数的恒等变换与性质，解三角形，将三角函数化成复合三角函数是关键．