重庆市高2024届高三第六次质量检测（2月）数学试卷答案,我们目前收集并整理关于重庆市高2024届高三第六次质量检测（2月）数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

重庆市高2024届高三第六次质量检测（2月）数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

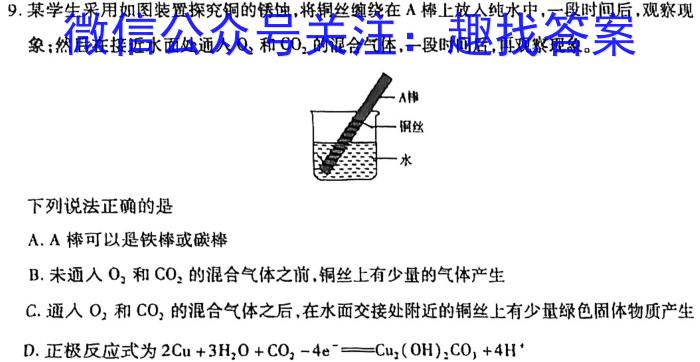
9.某学生采用如图装置探究铜的锈蚀,将铜丝缠绕在A棒上放人纯水中,一段时间后,观察现象;然后在接近水面处通人O2和CO2的混合气体,一段时间后,再观察现象。下列说法正确的是A.A棒可以是铁棒或碳棒B.未通入O2和CO2的混合气体之前,铜丝上有少量的气体产生C.通人O2和CO2的混合气体之后,在水面交接处附近的铜丝上有少量绿色固体物质产生D.正极反应式为2Cu+3H2O+CO2-4e^-Cu2(OH)2CO3+4H^-

分析（1）求得h（x）的导数，对a讨论，当a≤0时，当a＞0时，由导数大于0，可得增区间；由导数小于0，可得减区间；
（2）要证对任意n∈N^*，均有$\frac{{e}^{n}}{n!}$≤${e}^{1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}}$≤en．即证ln$\frac{{e}^{n}}{n!}$≤1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$＜ln（en），构造函数F（x）=lnx-$\frac{x-1}{x}$，求出导数，判断单调性，由累加法即可证得左边；再由数学归纳法证得右边．

解答解：（1）函数h（x）=f′（x）+g（x）=1+lnx+$\frac{a}{x}$-2（x＞0），
h′（x）=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$=$\frac{x-a}{{x}^{2}}$，
当a≤0时，h′（x）＞0，h（x）递增；
当a＞0时，h′（x）＞0，可得x＞a；h′（x）＜0，可得0＜x＜a．
综上可得，a≤0时，h（x）的增区间为（0，+∞）；
a＞0时，h（x）的增区间为（a，+∞），减区间为（0，a）；
（2）证明：要证对任意n∈N^*，均有$\frac{{e}^{n}}{n!}$≤${e}^{1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}}$＜en．
即证ln$\frac{{e}^{n}}{n!}$≤1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$＜ln（en），
先证ln$\frac{{e}^{n}}{n!}$≤1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$．
由F（x）=lnx-$\frac{x-1}{x}$的导数F′（x）=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$，
当x≥1时，F（x）递增，F（x）≥F（1）=0，
即为$\frac{1}{x}$≥1-lnx=ln$\frac{e}{x}$，
令x=1，2，3，…，n，累加可得，
1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$≥lne+ln$\frac{e}{2}$+…+ln$\frac{e}{n}$=ln$\frac{{e}^{n}}{n!}$；
再证1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$＜ln（en），
运用数学归纳法证明．
当n=1时，左边=1，右边=lne=1，成立；
假设n=k时，1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{k}$≤ln（ek），成立．
当n=k+1时，1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{k}$+$\frac{1}{k+1}$≤ln（ek）+$\frac{1}{k+1}$，
要证1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{k}$+$\frac{1}{k+1}$≤lne（k+1），
只要证ln（ek）+$\frac{1}{k+1}$≤lne（k+1），
即证$\frac{1}{k+1}$≤ln$\frac{k+1}{k}$=ln（1+$\frac{1}{k}$），
可令x=$\frac{1}{k}$∈（0，1]，即证ln（1+x）≥$\frac{x}{x+1}$，
由G（x）=ln（1+x）-$\frac{x}{x+1}$的导数为$\frac{1}{1+x}$-$\frac{1}{（x+1）^{2}}$=$\frac{x}{（x+1）^{2}}$＞0，
则G（x）在（0，1]递增，即有G（x）＞G（0）=0，
即有ln（1+x）≥$\frac{x}{x+1}$成立，故$\frac{1}{k+1}$≤ln$\frac{k+1}{k}$=ln（1+$\frac{1}{k}$），
综上可得1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$＜ln（en），
故原不等式成立．

点评本题考查导数的运用：求单调区间，考查不等式的证明，注意运用构造函数判断单调性，同时考查累加法和分类讨论的思想方法，以及数学归纳法的运用，属于难题．