百师联盟 2024届高三冲刺卷(一)1 (新教材)数学试卷答案,我们目前收集并整理关于百师联盟 2024届高三冲刺卷(一)1 (新教材)数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

百师联盟 2024届高三冲刺卷(一)1 (新教材)数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

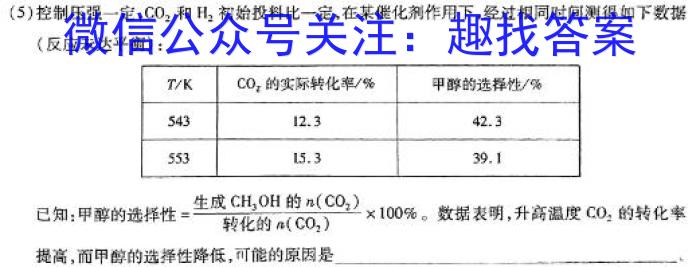
(5)控制压强一定,CO2和H2初始投料比一定,在某催化剂作用下,经过相同时间测得如下数据(反应未达平衡):CH3OH已知:甲醇的选择性生成Hg(n(CO2)n(CO2)100\%。%。数据表明,升高温度CO2的转化率提高,而甲醇的选择性降低,可能的原因是

分析（1）利用函数与方程的关系，求出a，然后得到函数的解析式，即可判断函数的奇偶性．
（2）通过函数的解析式以及定义域，求解函数的值域即可．
（3）$x∈[\frac{1}{2}，\frac{2}{3}]$，求出f（x）的最大值，利用 f（x）_max＞g（x）_max，求出k的范围即可．

解答解：（1）函数$f（x）={log_2}（\frac{1+ax}{1-x}）$，$f（\frac{1}{3}）=1$，可得$1=lo{g}_{2}（\frac{1+\frac{1}{3}a}{1-\frac{1}{3}}）$，解得$\frac{1+\frac{1}{3}a}{1-\frac{1}{3}}=2$，3+a=4，
∴a=1，
f（x）的解析式为：$f（x）=lo{g}_{2}（\frac{1+x}{1-x}）$，定义域为（-1，1）
$f（-x）=lo{g}_{2}（\frac{1-x}{1+x}）$=$-lo{g}_{2}（\frac{1+x}{1-x}）=-f（x）$，可知函数是奇函数；
（2）当x∈[-1，0）时，3^x∈$[\frac{1}{3}，1）$；$f（x）=lo{g}_{2}（\frac{1+x}{1-x}）$是增函数，$lo{g}_{2}（\frac{1+\frac{1}{3}}{1-\frac{1}{3}}）$=1，
f（3^x）∈[1，+∞）．
（3）$x∈[\frac{1}{2}，\frac{2}{3}]$，函数 f（x）的最大值：$f（\frac{2}{3}）=lo{g}_{2}（\frac{1+\frac{1}{3}}{1-\frac{2}{3}}）$=log₂5．
函数$g（x）={log_{\sqrt{2}}}\frac{k}{1-x}$，若存在$x∈[\frac{1}{2}，\frac{2}{3}]$使不等式 f（x）＞g（x）成立，
$g（x）=lo{g}_{\sqrt{2}}\frac{k}{1-x}$是增函数，g（x）＜$g（\frac{2}{3}）=lo{g}_{\sqrt{2}}\frac{k}{1-\frac{2}{3}}$=$lo{g}_{\sqrt{2}}3k$
可得$lo{g}_{2}5＞lo{g}_{\sqrt{2}}\frac{k}{1-x}$，$lo{g}_{2}5＞lo{g}_{\sqrt{2}}（3k）$，
可得：0＜k$＜\frac{\sqrt{5}}{3}$．

点评本题考查函数与方程的综合应用，函数的奇偶性以及函数的单调性，函数恒成立，考查转化思想以及计算能力．