安徽省池州市东至县2024届九年级上学期1月期末考试数学试卷答案,我们目前收集并整理关于安徽省池州市东至县2024届九年级上学期1月期末考试数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

安徽省池州市东至县2024届九年级上学期1月期末考试数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

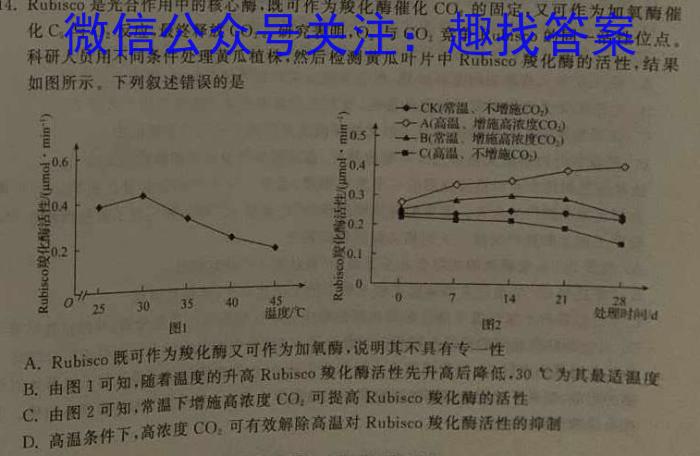
14.Rubisc是光合作用中的核心酶,既可作为羧化酶催化CO2的固定,又可作为加氧酶催化C5与O2反应,最终释放CO2。研究表明,O2与CO2竞争Rubisco的同一活性位点。科研人员用不同条件处理黄瓜植株,然后检测黄瓜叶片中Rubisco羧化酶的活性,结果如图所示,下列叙述错误的是CKl(常温、不增施CO2A(高温、增施高浓度(CO2)0.5一-B(常温,增施高浓度CO2-Cl高温、不增施(CO2)0.60.40.33H0.42.20.20.1071421282530354045处理时间图2图1A.Rubisco既可作为羧化酶又可作为加氧酶,说明其不具有专一性30^CB.由图1可知,随着温度的升高Rubisco羧化酶活性先升高后降低,30℃为其最适温度C.由图2可知,常温下增施高浓度CO,可提高Rubiseo羧化酶的活性CO2CO2RD.高温条件下,高浓度CO可有效解除高温对Rubisco羧化酶活性的抑制

分析由AB∥CD，AB=2CD得V_{三棱锥B-ACE}=2V_{三棱锥D-ACE}，由M是AE中点得V_{三棱锥B-ACM}=V_{三棱锥B-MCE}，故三棱锥M-EBC的体积为四棱锥体积的$\frac{1}{3}$．

解答解：∵AB∥CD，AB=2CD，
∴V_{三棱锥B-ACE}=2V_{三棱锥D-ACE}．
∵M为AE的中点，
∴S_△MCE=S_△ACM，
∴V_{三棱锥B-ACM}=V_{三棱锥B-MCE}，
∵V_{三棱锥B-ACE}=V_{三棱锥B-ACM}+V_{三棱锥B-MCE}，
∴V_{三棱锥B-ACM}=V_{三棱锥B-MCE}=V_{三棱锥D-ACE}，
∵V=V_{三棱锥B-ACM}+V_{三棱锥B-MCE}+V_{三棱锥D-ACE}，
∴V_{三棱锥M-EBC}=V_{三棱锥B-MCE}=$\frac{1}{3}$V．
故选C．

点评本题考查了几何体的体积，将四棱锥分解成三个体积相等得三棱锥是关键．