河北省遵化市2023-2024学年度第一学期七年级期末学业评估数学试卷答案,我们目前收集并整理关于河北省遵化市2023-2024学年度第一学期七年级期末学业评估数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

河北省遵化市2023-2024学年度第一学期七年级期末学业评估数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

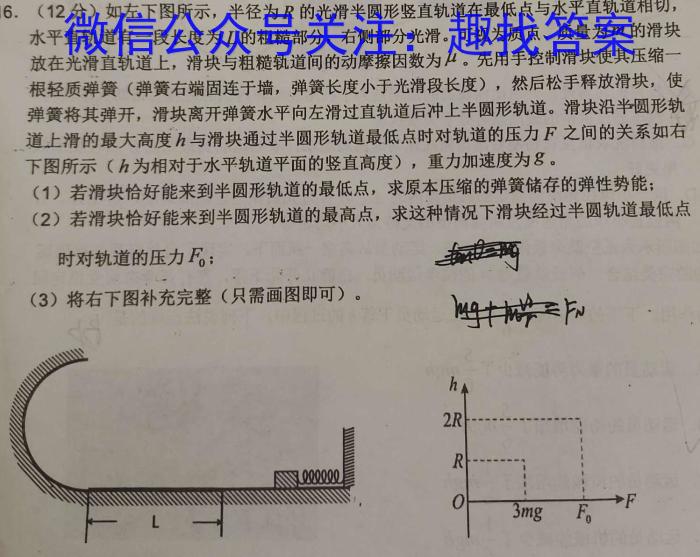
16.(12分)如左下图所示,半径为R的光滑半圆形竖直轨道在最低点与水平直轨道相切,水平直轨道有一段长度为L的粗糙部分,右侧部分光滑。可视为质点、质量为m的滑块放在光滑直轨道上,滑块与粗糙轨道间的动摩擦因数为先用手控制滑块使其压缩一根轻质弹簧(弹簧右端固连于墙,弹簧长度小于光滑段长度),然后松手释放滑块,使弹簧将其弹开,滑块离开弹簧水平向左滑过直轨道后冲上半圆形轨道。滑块沿半圆形轨道上滑的最大高度h与滑块通过半圆形轨道最低点时对轨道的压力F之间的关系如右下图所示(h为相对于水平轨道平面的竖直高度),重力加速度为8。(1)若滑块恰好能来到半圆形轨道的最低点,求原本压缩的弹簧储存的弹性势能;(2)若滑块恰好能来到半圆形轨道的最高点,求这种情况下滑块经过半圆轨道最低点时对轨道的压力F0;(3)将右下图补充完整(只需画图即可)。h2RR3m>FLLmgF

分析（1）根据函数解析式恒有意义，可得函数f（x）=$\frac{a}{{a}^{2}-1}$（a^x-a^-x）的定义域为R；任取x₁＜x₂，作差f（x₁）-f（x₂）并判断符号，结合函数单调性的定义，可得f（x）在R上的单调性递增；
（2）若F（x）=f（x）-4且在（-∞，2]上恒有F（x）＜0，则F（2）=$\frac{a}{{a}^{2}-1}$（a²-a^-2）-4＜0，解得答案．

解答解：（1）∵f（x）=$\frac{a}{{a}^{2}-1}$（a^x-a^-x）（a＞0且a≠1）
对于任意x∈R，函数的解析式均有意义，
故函数f（x）=$\frac{a}{{a}^{2}-1}$（a^x-a^-x）的定义域为R；
f（x）=$\frac{a}{{a}^{2}-1}$（a^x-a^-x）在R为上增函数，理由如下：
设x₁＜x₂，
∴f（x₁）-f（x₂）=$\frac{a}{{a}^{2}-1}$（a^x₁-a^-x₁）-$\frac{a}{{a}^{2}-1}$（a^x_2-a^-x₂）=$\frac{a}{{a}^{2}-1}$（a^x₁-a^x₂）（1+$\frac{1}{{a}^{{x}_{1}}•{a}^{{x}_{2}}}$）=$\frac{a}{{a}^{2}-1}$（a^x₁-a^x₂）（1+$\frac{1}{{a}^{{x}_{1+{x}_{2}}}}$），
∵0≤x₁＜x₂，
①当0＜a＜1时，$\frac{a}{{a}^{2}-1}$＜0，a^x₁＞a^x₂，1+$\frac{1}{{a}^{{x}_{1+{x}_{2}}}}$＞0，
∴f（x₁）-f（x₂）＜0，即f（x₁）＜f（x₂），
∴f（x）在R上的单调性递增；
②当a＞1时，$\frac{a}{{a}^{2}-1}$＞0，a^x₁＜a^x₂，1-$\frac{1}{{a}^{{x}_{1+{x}_{2}}}}$＞0，
∴f（x₁）-f（x₂）＜0，即f（x₁）＜f（x₂），
∴f（x）在R上的单调性递增；
（2）F（x）=f（x）-4在（-∞，2]上也为增函数，
若F（x）＜0恒成立，则F（2）=$\frac{a}{{a}^{2}-1}$（a²-a^-2）-4＜0，
即a-a^-1-4＜0，即a²-4a-1＜0，
解得：2-$\sqrt{5}$＜a＜2+$\sqrt{5}$，
又由a＞0且a≠1得：a∈（0，1）∪（1，2+$\sqrt{5}$）．

点评本题考查的知识点是函数单调性的性质，函数单调性的判断与证明，恒成立问题，难度中档．