河北省2023-2024学年第一学期高二年级二调考试(242429D)数学试卷答案,我们目前收集并整理关于河北省2023-2024学年第一学期高二年级二调考试(242429D)数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

河北省2023-2024学年第一学期高二年级二调考试(242429D)数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

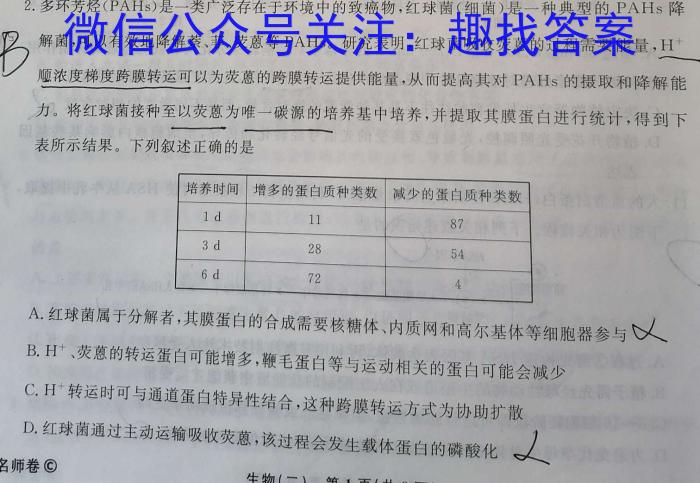
2.多环芳烃(PAHs)是一类广泛存在于环境中的致癌物,红球菌(细菌)是一种典型的PAHs降8解菌,可以有效地降解萘、菲、荧蒽等PAHs。,研究表明,红球菌吸收荧蒽的过程需要能量,H^+顺浓度梯度跨膜转运可以为荧蒽的跨膜转运提供能量,从而提高其对PAHs的摄取和降解能力。将红球菌接种至以荧蒽为唯一碳源的培养基中培养,并提取其膜蛋白进行统计,得到下表所示结果。下列叙述正确的是A.红球菌属于分解者,其膜蛋白的合成需要核糖体、内质网和高尔基体等细胞器参与B.H^+、荧蒽的转运蛋白可能增多,鞭毛蛋白等与运动相关的蛋白可能会减少C.H^+转运时可与通道蛋白特异性结合,这种跨膜转运方式为协助扩散D.红球菌通过主动运输吸收荧蒽,该过程会发生载体蛋白的磷酸化

分析（1）先求出当α=$\frac{π}{4}$，直线L为：y=x-1，圆C：x²+y²=4，联立$\left\{\begin{array}{l}{y=x-1}\\{{x}^{2}+{y}^{2}=4}\end{array}\right.$，得2x²-2x-3=0，利用韦达定理能求出直线L与圆C交点的中点坐标为（$\frac{1}{2}，-\frac{1}{2}$）．
（2）直线L过定点P（1，0），圆C是圆心C（0，0），半径r=2的圆，由|PC|=1＜2=r，能证明直线L与圆C相交．当相交弦与PC垂直时，相交弦最短．

解答解：（1）∵直线L：$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$（t为参数），
∴$\frac{y}{x-1}$=tanα，
当α=$\frac{π}{4}$，直线L为：y=x-1，
∵圆C：$\left\{\begin{array}{l}{x=2cosθ}\\{y=2sinθ}\end{array}\right.$（θ为参数），∴x²+y²=4，
∴圆C是圆心C（0，0），半径r=2的圆，
联立$\left\{\begin{array}{l}{y=x-1}\\{{x}^{2}+{y}^{2}=4}\end{array}\right.$，得2x²-2x-3=0，
直线L与圆交于A（x₁，y₁），B（x₂，y₂），
则x₁+x₂=1，y₁+y₂=（x₁-1）+（x₂-1）=1-2=-1，
∴直线L与圆C交点的中点坐标为（$\frac{1}{2}，-\frac{1}{2}$）．
证明：（2）∵直线L：$\frac{y}{x-1}$=tanα，∴直线L过定点P（1，0），
∵圆C是圆心C（0，0），半径r=2的圆，
∴|PC|=1，∵|PC|=1＜2=r，
∴直线L与圆C相交．
当相交弦与PC垂直时，相交弦最短，
∴最短弦的长度d_min=2$\sqrt{{r}^{2}-|PC{|}^{2}}$=2$\sqrt{3}$．

点评本题考查直线与圆相交弦中点坐标的求法，考查直线与圆垂直的证明，考查相交弦最短时其长度的求法，是中档题，解题时要认真审题，注意点到直线距离公式的合理运用．