衡水金卷先享题2024年普通高等学校招生全国统一考试模拟试题分科综合全国乙卷数学试卷答案,我们目前收集并整理关于衡水金卷先享题2024年普通高等学校招生全国统一考试模拟试题分科综合全国乙卷数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

衡水金卷先享题2024年普通高等学校招生全国统一考试模拟试题分科综合全国乙卷数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

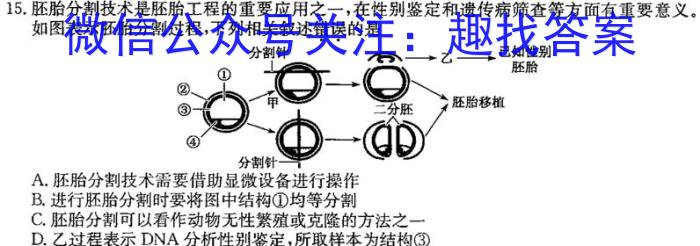
15.胚胎分割技术是胚胎工程的重要应用之一,在性别鉴定和遗传病筛查等方面有重要意义。如图表示胚胎分割过程,下列相关叙述错误的是A.胚胎分割技术需要借助显微设备进行操作B.进行胚胎分割时要将图中结构①均等分割C.胚胎分割可以看作动物无性繁殖或克隆的方法之一D.乙过程表示DNA分析性别鉴定,所取样本为结构③

分析（1）分段求出函数g（x）的表达式，再综合得g（x）=$\left\{\begin{array}{l}{-{2}^{-x}，x＞0}\\{0，x=0}\\{{2}^{x}，x＜0}\end{array}\right.$；
（2）根据题设可得，g（x）=$\frac{ax+b}{x+1}$的取值能包含[1，2），且g（0）=1，当x→+∞时，g（x）=$\frac{a+\frac{b}{x}}{1+\frac{1}{x}}$→a=2．

解答解：（1）因为g（x）为f（x）的延拓函数，且g（x）为奇函数，所以，
①当x＜0时，g（x）=f（x）=2^x，②当x=0时，g（x）=0，③当x＞0时，g（x）=-f（-x）=-2^-x，
综合以上讨论得，所以，g（x）=$\left\{\begin{array}{l}{-{2}^{-x}，x＞0}\\{0，x=0}\\{{2}^{x}，x＜0}\end{array}\right.$；
（2）当x＜0时，g（x）=f（x）=2^x∈（0，1），且x→0时，g（x）→1，
由于g（x）的值域为（0，2），
所以，当x≥0时，g（x）=$\frac{ax+b}{x+1}$的取值能包含[1，2），
又∵对于任意的x₁，x₂∈R，且x₁≠x₂，都有$\frac{g（{x}_{1}）-g（{x}_{2}）}{{x}_{x}-{x}_{2}}$＞0，
∴g（x）在R上单调递增，所以，g（0）=1，解得b=1，
当x→+∞时，g（x）=$\frac{a+\frac{b}{x}}{1+\frac{1}{x}}$→a，故a=2，
因此，当x≥0时，g（x）=$\frac{ax+b}{x+1}$=$\frac{2x+1}{x+1}$．
故答案为：（1）g（x）=$\left\{\begin{array}{l}{-{2}^{-x}，x＞0}\\{0，x=0}\\{{2}^{x}，x＜0}\end{array}\right.$；（2）a=2，b=1．

点评本题主要考查了函数性质的综合应用，涉及函数的奇偶性，解析式，单调性，值域，以及分段函数的表示，属于中档题．