山西省2023~2024学年第一学期八年级期中学业诊断数学试卷答案,我们目前收集并整理关于山西省2023~2024学年第一学期八年级期中学业诊断数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

山西省2023~2024学年第一学期八年级期中学业诊断数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

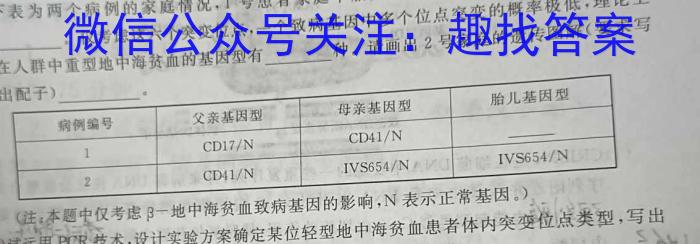
(2)下表为两个病例的家庭情况,1号患者家庭中胎儿患上重型地中海贫血的概率为。仅考虑这六个突变位点,一个致病基因中多个位点突变的概率极低,理论上在人群中重型地中海贫血的基因型有种。请画出2号家庭的遗传图解(要求写出配子)。(注:本题中仅考虑β一地中海贫血致病基因的影响,N表示正常基因。)

分析由a_n+2+a_ncosnπ=1，当n=2k-1时，k∈Z，a_2k+1-a_2k-1=1，可得数列{a_2k-1}是首项为1，公差为1的等差数列．当n=2k时，k∈Z，a_2k+2+a_2k=1．可得S₁₂₀．又a₆₁=31，即可得出．

解答解：由a_n+2+a_ncosnπ=1，当n=2k-1时，k∈Z，a_2k+1-a_2k-1=1，∴数列{a_2k-1}是首项为1，公差为1的等差数列．
∴a₁+a₃+…+a₁₁₉=$\frac{（1+60）×60}{2}$=1830．
当n=2k时，k∈Z，a_2k+2+a_2k=1．
∴a₂+a₄+…+a₁₂₀=（a₂+a₄）+（a₆+a₈）+…+（a₁₁₈+a₁₂₀）=30．
∴S₁₂₀=1830+30=1860．
又a₆₁=a_2×30+1=1+30=31，
∴$\frac{{S}_{120}}{{a}_{61}}$=$\frac{1860}{31}$=60．
故选：C．

点评本题考查了等差数列的定义及其前n项和公式、“分组求和”，考查了推理能力与计算能力，属于中档题．