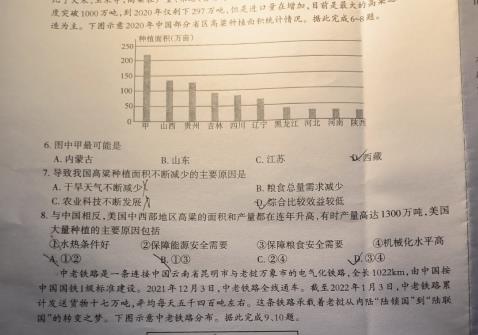
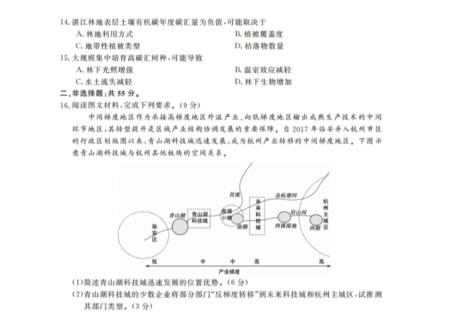
贵州省2024届贵阳一中高考适应性月考一(白黑黑黑白白白)数学答案,目前2024天舟益考答案网已经汇总了贵州省2024届贵阳一中高考适应性月考一(白黑黑黑白白白)数学答案的各科答案和试卷,更多2024天舟益考答案网请关注本网站。

1点已知曲线)-alnr(a∈R)与曲线g)=石在公共点处有共同的切线,则实数a的值为20.(本小题满分12分)16.传说中孙悟空的“如意金箱棒”"是由"定海神针”变形得来的这定海神针在变形时永远保持为圆柱每个国家对退休年龄都有不样的规定,从2018年开始我国关于廷迟退休的话题一直在网体,其底面半径原为12m且以每秒1m等速率缩短,而长度以每秒20m等速率增长已知神上热议,为了了解市民对延迟退休”的态度,现以某地市民中能机选取0人进行调查,调针的底面半径只能从12m缩到4m为止.已知在这段变形过程中,当底面半径为10cm时其体查情况如下表:[15,25)积最大年龄段(单位:岁)[25,35)[35,45)被调查的人数10[45,55)[55,65)(1)该定海神针原来的长度为6[65,75)cm;20m25(2)假设孙悟空将神针体积最小时定形成金箍棒,则此时金箍棒的底面半径为,赞成的人数612126cm.(第一空2分,第二空3分)四、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤,4)从赞成“延迟退休”的人中任选1人此人年龄在[35,45)的概率为员,求出表格中m,17.(本小题满分10分)的值;在△ABC中,角A,B,C所对的边分别为a,bc,已知血A二血S=“-sin A+sin B c(2)在被调查的人中,年龄低于35岁的人可以认为“低龄人”,年龄不低于35岁的人可以认(1)求角B的大小:为“非低龄人”,试作出是否赞成“延迟退休”与“低龄与否”的2×2列联表,并指出是否有(2)设m=2a一c,若b=3,且A,C都为锐角,求m的取值范围。99%的把握认为赞成“延迟退休”与“年龄”有关,并说明理由。n(ad-bc)2附:K2=(a+b)(c+D(a+c)(b+dn=a+b+c+d.P(K2>)0.1000.0500.0100.005ko2.7063.8416.6357.87918.(本小题满分12分)在数列(an中,a1=1,a2=3,且对任意的n∈N,都有a1=3a1一2a(1)证明:数列(a1一a,是等比数列,并求数列{a.的通项公式,21.(本小题满分12分)(2)b,=a,一入,若数列(b,)是单调递增数列,求实数入的取值范围。已知双曲线C号一-苦-1。>0,6>0的建特长为4,直线2一)y一0为双曲线C的条新近线(1)求双曲线C的标准方程;(2)记双曲线C的左、右顶点分别为A,B,过点T(2,0)的直线1交双曲线C于点M,N(点19.(本小题满分12分)M在第一象限),记直线MA斜率为k,直线NB斜率为k:,求证:是为定值如图3所示的多面体是由三棱锥A一BDE与四棱锥D一BCFE对接而成,其中EF⊥平面AEB,AE⊥EB,AD∥EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点,22.(本小题满分12分)(I)求证:BD⊥EG,已知函数fx)=ln1+mx),g)=-+u(2)求平面DEG与平面AEFD所成锐二面角的余弦值(1)当m=1时,求函数F(x)=fx)-x的最大值,(2)当0<m<1时,判断函数G(x)=f(x)-g(x)的零点个数.【2022冲刺押题卷·数学(六)第3页(共4页)新高考】【2022冲刺押题卷·数学(六)第4页(共4页)新高考】
[db:内容2]